1350 Limits

Math 1350 - Limits and continuity

MAPLE has a powerful capability to find a limit. The MAPLE function that is used to find a limit is limit.

Example1:

find the limit of f(x) = (x-2)/(x^2-1)

First define the function f(x)

> f:=x->(x-2)/(x^2 - 1);

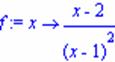
Find the limit of f(x) as x approaches 0, 1, -1, infinity

> limit(f(x), x=0);

> limit(f(x), x=1);

> limit(f(x), x=-1);

> limit(f(x), x=infinity);

When x approaches 1, -1 the limit does not exist therefore MAPLE gives undefined.

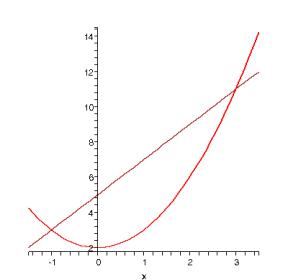
To convince ourselves about the function´s behavior we can plot it.

> plot(f(x), x=-10..10, y=-10..10);

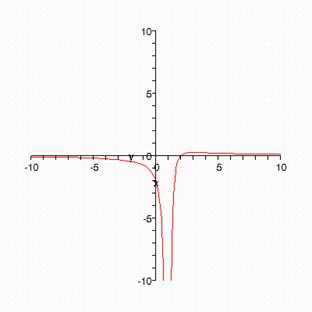
Example2:

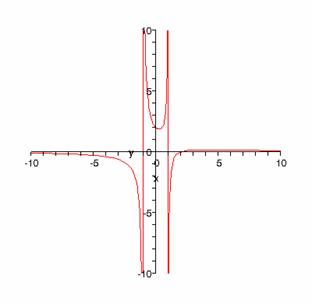
a different behavior has the limit of f(x) = (x-2)/(x-1)^2.

> f:=x->(x-2)/(x - 1)^2;

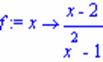
> limit(f(x), x=0);

> limit(f(x), x=1);

> limit(f(x), x=-1);

> limit(f(x), x=infinity);

> plot(f(x), x=-10..10, y=-10..10);

Example3:

find the limit of f(x)=|x| as x -> 0. To write in MAPLE the absolute value of x, use the command abs.

> f:=x->abs(x);

> limit(f(x), x=0);

Example3:

define f(x) = sin(1/x). Find the limit as x -> 0, and as x -> infinity. Plot the function.

> f:=x->sin(1/x);

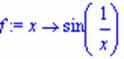
> limit(f(x), x=0);

> limit(f(x), x=infinity);

> plot(f(x), x=-10..10, y=-1.5..1.5);

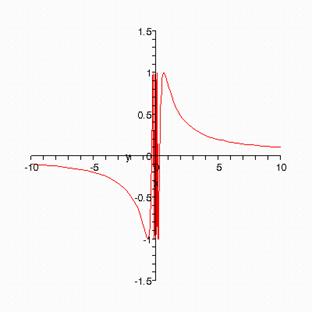
f(x) is not continuous at as x -> 0 because its limit is ?1..1. It is continuous everywhere else since limit f(x) = 0 as x -> .

Exercises:

Find the limit of the fallowing functions a) as x -> 0; b) as x->. Plot them.